In geometry, the tangent line (or simply tangent) to a plane curve at a given point is, intuitively, the straight line that "just touches" the curve at that point.
Sine, Cosine and Tangent are the main functions used in Trigonometry and are based on a Right-Angled Triangle. Before getting stuck into the functions, it helps to give a name to each side of a right triangle: Opposite is always opposite the angle. And Adjacent is always next to the angle.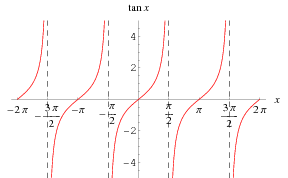
The tangent function is defined by tanx= (sinx)/ (cosx), (1) where sinx is the sine function and cosx is the cosine function. The notation tgx is sometimes also used (Gradshteyn and Ryzhik 2000, p. xxix).